Глава II. ОСДСС. Формирование орбиты в процессе захвата спутника.

В  первой главе "ОСДСС, Принцип захвата" утверждается, что все спутниковые системы от простейших типа системы Марса (небольшая планета с двумя миниатюрными спутниками) до гигантских скоплений галактик, образуются одним путем – путем захвата каким– либо массивным телом (системой тел) другого тела (системы тел). Захват происходит в том случае, когда будущий спутник (будем рассматривать его как тело точечное, если это даже и система тел) пытается пройти мимо более массивного тела (экспанта) на определенном расстоянии L и с определенной скоростью V, благоприятными для захвата. По связи с экспантом захватываемый объект будем называть для краткости пантексом.

Расстоянием L в данном случае является длина перпендикуляра ЭТ, опущенного из центра экспанта на прямую, продолжающую начальное направление движения пантекса в околоэкспантном пространстве (рис.5). Это расстояние равно среднему радиусу будущей орбиты спутника, то есть L=ЭТ=R ср. На рис. 5 положение экспанта обозначено точкой Э, а равенство ЭТ=R ср. не выдержано.

Математически условия захвата описываются формулой захвата 

R · V²= Μ · γ, где  М – масса экспанта.

В процессе захвата исходным положением для пантекса является равномерное прямолинейное движение. Как и где возникло тело, какую оно имеет форму, чем вызвано его движение – вопросы преждевременные. Ответ на них будет предложен позже. А пока равномерное прямолинейное движение пантекса в направлении мимо экспанта – условие заданное.

В некоторой точке А  пантекс входит в дальние окрестности гравитационного поля экспанта. На него начинает оказывать влияние сила притяжения экспанта центростремительная сила G, сообщающая пантексу нормальное ускорение Wn. Поскольку сила притяжения пантекса действует в направлении центра экспанта, то пантекс вскоре отклоняется от начального пути и переходит с прямолинейного движения на криволинейное.

По мере сокращения расстояния между экспантом и пантексом центростремительная сила, обратно пропорциональная квадрату расстояния, быстро увеличивается –              

Здесь М  и m – массы взаимодействующих тел.

Так же быстро растет и нормальное, направленное к экспанту, ускорение пантекса Wn, а вместе с ним и скорость тела V.

       В свою очередь с увеличением скорости движения пантекса растет его сила инерции – центробежная сила Р, прямо пропорциональная квадрату скорости пантекса                              

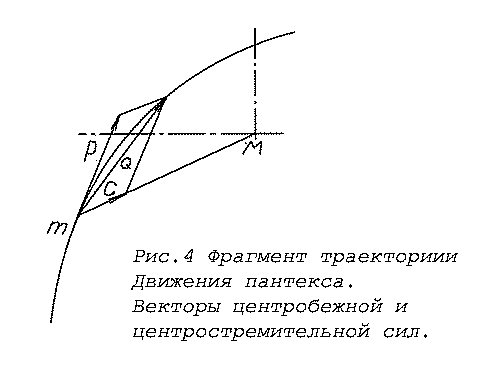
а вместе с ней и тангенциальное ускорение Wτ.

Центробежная сила – сила консервативная. Она стремится сохранить начальное состояние тела и всегда направлена по касательной в каждой точке траектории движения пантекса. Противоборство разнонаправленных центробежной и центростремительной сил порождает силу результирующую и формирует траекторию движения пантекса.

Центростремительная сила G и нормальное ускорение Wn по законам теоретической механики схематически изображаются векторами, показывающими направление действия  (к центру экспанта) и их относительную величину. Центробежная сила Р и тангенциальное ускорение Wτ направлены по касательной к траектории движения захватываемого тела и также изображаются соответствующими векторами.

Результирующая сила Q и ускорение W находятся графически из полученного параллелограмма по правилу сложения векторов (рис.4).  

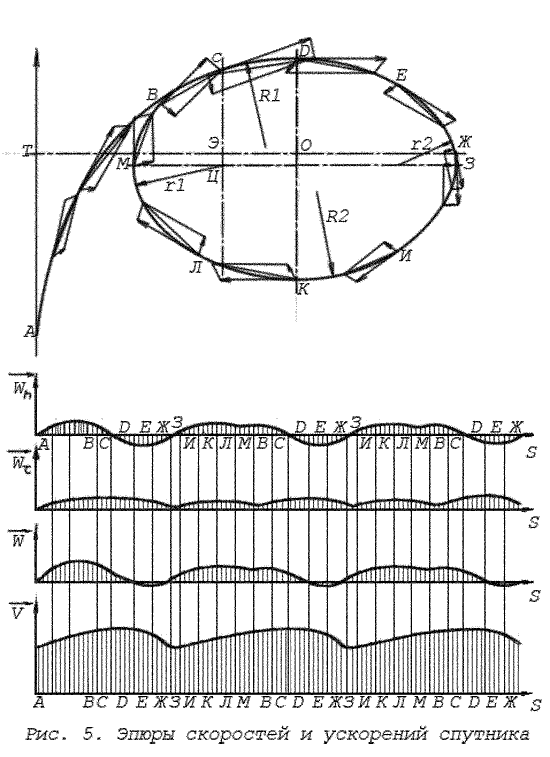
При этом направление результирующей силы (ускорения) показывает фактическое направление движения захваченного тела (пантекса) непосредственно в каждой точке его траектории.

Пользуясь приемами теоретической механики, я исследовал типичную траекторию условного пантекса по ее экстремальным точкам. Экстремальными являются такие точки траектории движения пантекса, в которых центробежная, центростремительная или результирующая сила, нормальное, тангенциальное или результирующее ускорение спутника достигают предельных, максимальных или минимальных, значений или меняют знак на обратный.

При исследовании траектории пантекса, переходящей в замкнутую орбиту спутника, выявлено таким образом 11 экстремальных точек и 10 характерных участков,  присущих изначально всем спутниковым орбитам. Результаты исследования в полном объеме здесь не приводятся из–за обилия материала. Но присмотреться к наиболее важным точкам и формообразующим  участкам орбиты спутника все–таки придется. Это нужно для того, чтобы понять специфику образования спутниковых орбит, их характерные особенности.

Поскольку нормальное ускорение Wn есть величина, производная от центростремительной силы и пропорционально этой силе, а тангенциальное ускорение Wτ – пропорционально центробежной силе, при этом векторы направлений соответствующих сил и ускорений тоже полностью совпадают, то далее для упрощения картины будем оперировать понятиями ускорений.

На исходном участке AB траектории (рис.5) нормальное Wn, тангенциальное Wτ и результирующее W ускорения пантекса стремительно растут. Так же стремительно растет и его скорость. Этот участок я называю участком абсолютного ускорения. Но уже в точке В происходят первые перемены. С этой точки нормальное ускорение Wn , оставаясь величиной положительной, начинает постепенно снижаться – проекция вектора нормального ускорения на вектор ускорения результирующего становится меньше, так как увеличивается угол между этими векторами. Тем не менее пантекс продолжает набирать скорость, поскольку результирующее ускорение на участке ВС по прежнему растет в высоком темпе.

Точка С – ближайшая к экспанту точка траектории пантекса, перигелий. Она близка к точке, в которой вертикальная центровая линия, проведенная через экспант, пересекает траекторию пантекса. Но С интересна еще и тем, что в этой точке проекция нормального ускорения Wn  на результирующее W также обращается в точку. С точки С и далее Wn  уже не действует на пантекс ускоряюще. Оно становится величиной отрицательной и начинает тормозить движение пантекса. Однако скорость пантекса в этой ближайшей к экспансу точке достигает такой большой величины, что пантекс легко отрывается от экспанта и устремляется прочь от него чуть ли не по прямой (по кривой с максимальным радиусом закругления орбиты R1). Примечательно, что он удаляется от экспанта с продолжающей возрастать скоростью.

Подобная аномалия объясняется тем, что на всем участке СД тангенциальное ускорение Wτ, достигшее максимального значения в точке С и медленно снижающееся, остается тем не менее весьма высоким. Вследствие этого остается положительным и результирующее ускорение W. А коль скоро результирующее ускорение все еще положительно, то и скорость пантекса продолжает расти. Лишь в точке Д она достигает максимального значения и ее дальнейший рост прекращается.

 В точке Д поперечная осевая линия эллипса, представляющего собой будущую орбиту спутника, пересекает траекторию пантекса. Важнейший участок СД я называю участком перебега. Именно он, участок перебега, делает орбиту спутника эллипсообразной и порождает ее эксцентриситет, оставляя экспант в положении, близком к фокусу эллипса орбиты. Не будь этого участка –   экспант находился бы в центре эллипса орбиты спутника, а не в области его фокуса. Образование участка перебега при захвате спутника столь же неизбежно, как неизбежно ускорение пантекса при его приближении к экспанту, как неизбежна инерция движущегося тела.

Но ведь все спутники во всех спутниковых системах обращаются вокруг своих экспантов по эллипсообразным орбитам. При этом экспанты неизменно располагаются не в центре эллипсов орбит своих спутников, а в области их фокусов. Это может означать только одно: все спутники во всех спутниковых системах стали таковыми не иначе, как в результате захвата.

Впрочем, не все так просто. Известно немалое число спутников, обращающихся вокруг своих эспантов по круговым, так называемым регулярным орбитам. Такие спутники есть у крупных планет Солнечной системы Юпитера, Сатурна, Урана.

Чем объясняется это противоречие? А тем, что все это старые спутники. Их круговые орбиты в свое время представляли собой те же эллипсы, но с течением времени в ходе естественной эволюции они утратили первоначальные специфические свойства. О неизбежности, о закономерности такой эволюции речь пойдет в следующей главе. А пока проследуем дальше по траектории движения пантекса. Точкой Д заканчивается участок АВСД, который представляет собой участок разгона пантекса.

 На участке ДЕЖ нормальное ускорение Wn отрицательно, тангециальное ускорение Wτ продолжает интенсивно падать. Отрицательно и результирующее ускорение. Это наглядно видно на эпюрах ускорений (рис.5). В итоге на всем участке ДЕЖ происходит последовательное снижение скорости пантекса. Это участок торможения. 

В точке Ж скорость пантекса снижается до некоторой критической величины. Это самая удаленная точка орбиты, афелий. Она лежит на пересечении продольной оси эллипса орбиты с траекторией движения пантекса. Пантекс обессилен. Он в значительной мере потерял инерцию, не способен на дальнейший отрыв от экспанта и круто разворачивается для движения в обратном направлении.

В точке Ж прекращается тормозящее действие нормального ускорения Wn. Начиная с этой точки, Wn  принимает положительное значение и начинает медленно расти. Тем не менее на коротком участке ЖЗ продолжается снижение скорости пантекса, хотя уже включен и действует ускоритель – положительно направленное Wn. Все тот же закон инерции образует новый участок перебега, участок, параллельный поперечной оси эллипса.

Подобно тому, как участок перебега СД обеспечивает смещение экспанта от центра эллипса в направлении его фокуса – ЭО, участок ЖЗ обеспечивает смещение экспанта относительно продольной оси эллипса – ЭЦ. Это смещение невелико. В планетных орбитах оно исчезающе мало, поэтому не удивительно, что астрономическая наука не подозревает о его существовании. Но так обстоит дело только с планетными орбитами. В орбитах комет и астероидов, в особенности комет долгопериодических, поперечное смещение экспанта (Солнца) относительно продольной оси эллипса должно быть весьма существенным.

Начиная с точки З и далее по мере сокращения расстояния до экспанта нормальное ускорение пантекса перманентно растет, а вместе с ним растет и скорость захваченного объекта. По ходу траектории пантекса еще встречаются экстремальные точки, в которых происходят определенные изменения (снижается или, напротив, растет нормальное ускорение), но в целом участок ЗИКЛМВ представляет собой участок разгона, аналогичный по функции участку АВ.

По завершении полного оборота вокруг экспанта пантекс приходит в точку В с той же скоростью, с какой он подошел к ней при первом сближении с экспантом. Дальнейшее движение пантекса идет по замкнутой орбите и превращается уже в движение спутника.

Образовавшаяся эллипсоподобная фигура орбиты захваченного тела отличается от классического кеплеровского эллипса и по форме больше похожа на проекцию яйца с его тупым и острым окончаниями. При этом экспант неизменно располагается в тупом конце "яйца", а на вершине острого конца находится точка афелия.

Разница в радиусах закруглений концов "яйца" такова, что не может остаться незамеченной: r1>>r2. Отличают орбиту спутника от правильного эллипса и другие ее элементы. В частности, нельзя не отметить разницу также и в радиусах закруглений продольных сторон "яйца": R1 > R2. Астрономы, естественно, знают об очевидных этих отличиях. Орбиты, у которых отличия от правильного эллипса  особенно заметны, они называют возмущенными, полагая, что нарушения формы орбиты вызваны влиянием каких–то других невидимых, может быть, тел.

Длительное и пристальное внимание астрономов приковал  к себе Уран. В поисках виновников возмущения его орбиты звездочеты обнаружили сначала Нептун, а потом и Плутон. Это событие было воспринято ученым миром как триумф, как торжество научной мысли. Вскоре, однако, выяснилось, что открытые таким образом планеты не дают удовлетворительного объяснения странностям в поведении Урана. Стали искать Трансплутон – гиганта с достаточно большой массой. Но продолжительные поиски предполагаемой планеты оказались тщетными. Тайны своей Уран не раскрыл. Более того, к загадке о форме орбиты добавилась другая: о скорости движения планеты. "….Фактическое движение Урана (1781…..1832 г.г.) не отвечает кеплеровскому движению плюс возмущения от планет…..Наблюдаемые отклонения в движении Урана имеют характер колебаний…….." –констатируют доктора ф.м. наук Е.А. Гребенников и Ю.А. Рябов в работе "Загадки движения Урана и открытие Нептуна".

Используя методику теоретической механики, я построил по экстремальным точкам траектории движения пантекса эпюры нормального и тангенциального ускорений (рис.5).Сложив эпюры этих ускорений, получил эпюру ускорения результирующего, по которой выстроилась итоговая эпюра скоростей пантекса. Эта эпюра наглядно показывает как, в каких точках, по какому закону изменяется скорость спутника на орбите, скорость тела, претерпевшего захват. Изменения скорости спутника определенно имеют характер колебаний, характер цикличных колебаний.

Не по тому же ли закону меняется скорость Урана на его возмущенной орбите? Нет сомнений, что по тому самому. По закону спутника, ставшего таковым в результате захвата.

<<< назад                                               далее >>>