ЗВЕЗДНАЯ МЕХАНИКА

Глава V.ОСДСС. Природа вращения небесных тел.

Глава VI.ОСДСС. Плотность вещества небесных тел и определяющие её факторы.

Глава VII.ОСДСС. Возникновение и первоначальный облик планет.

Глава VIII.Иллюзия расширения Вселенной. Миф о Большом Взрыве.

Глава IX.Захват в мире звёзд. Парные и кратные звёзды, шаровые скопления, галактики по теории захвата.

Глава X.Гамма–всплески. Грандиозная цепная реакция катастроф и её созидательная роль во Вселенной.

Глава XI.Гравитация. Видимое и сущее.

Глава XII.Рождение звёзд. Подлинный возраст звёзд и галактик.

Глава XIII.Квазар – агонизирующая галактика.

Глава XIV.Стационарная Вселенная. Итоги.

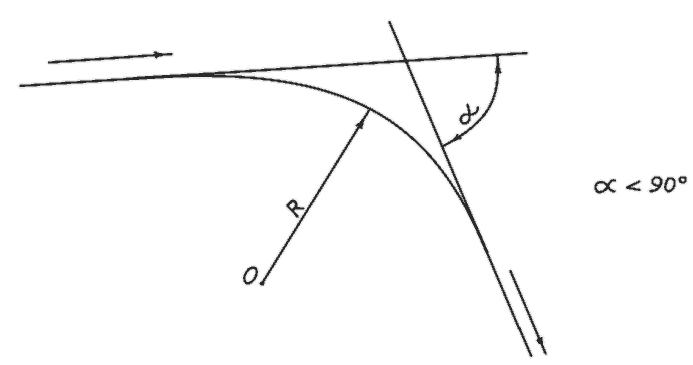
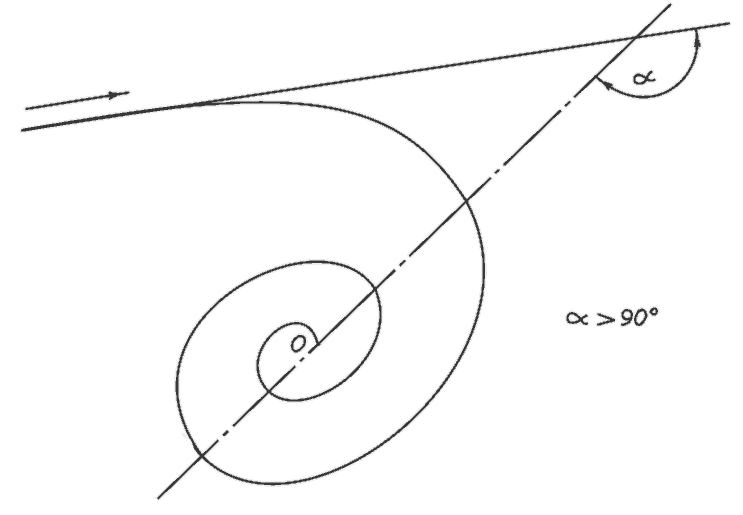
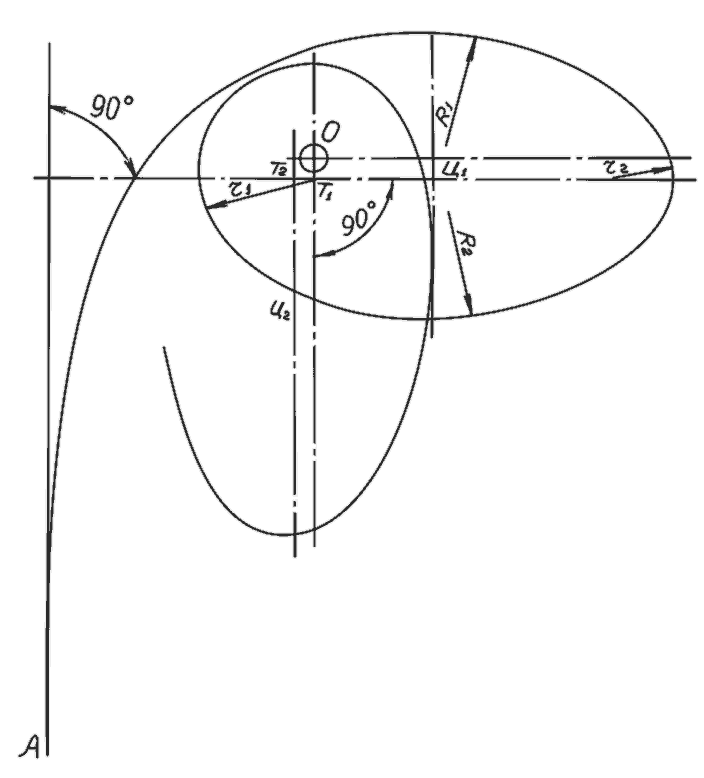
Глава I.Образование Солнечной и других спутниковых систем

(далее ОСДСС). Принцип захвата.

Мир, в котором живёт человек, интересен и многообразен. К тому же он ещё и сказочно красив. Кто не восхищался утренней зарёй, плывущими в зените облаками, семицветной радугой над зелёным лугом.

Есть на что посмотреть, есть чему подивиться на нашей планете. Но я не знаю зрелища более прекрасного, более величественного, более волнующего душу человеческую, чем звездное небо в ясную ночь.

Звёзды яркие и еле видимые, голубые и оранжевые, спокойные и мерцающие с пещёрных времён завораживали человека, будили его воображение своей таинственностью и недосягаемостью. Многие отважные умы откликались на этот зов, пытаясь понять окружающий мир, составить о нём всеохватное представление. Их усилия не были напрасными. Сегодня человек знает о Вселенной многое. Он заглянул в её глубину на расстояния, измеряемые миллиардами световых лет. Это чудовищные расстояния, которые невозможно даже вообразить.

Особенно хорошо человек изучил Солнечную систему – наш маленький тёплый очаг в суровой безбрежности Вселенной. Но мало знать устройство мира. Хочется знать больше – как возник, как сформировался этот мир. И, разумеется, прежде всего хотелось бы понять, как образовалась Солнечная система. На этот счёт было выдвинуто немало гипотез. Увы, ни одна из них не прошла проверку временем. Новые факты, новые знания опровергали стареющие представления. Та же участь постигла и последнюю по времени гипотезу О. Ю. Шмидта.

По версии Шмидта Солнечная система с планетами и их спутниками, с кометами и астероидами сформировалась в едином процессе из единого газо–пылевого облака. И хотя в представлениях об образовании небесных систем некоторые астрономы и ныне продолжают придерживаться гипотезы Шмидта, в широкие круги искателей истины пришло разочарование. Слишком многое из того, что мы знаем сегодня о Солнечной системе, не вписывается в газо–пылевую гипотезу. Астрономы озабочены. "Солнечная система устроена столь сложно, что постичь пути её образования в обозримом будущем не представляется возможным" – сетуют пессимисты.

Что и говорить, небесные миры – творения древние. В них всё – секрет и тайна. Начала и концы, причины и следствия затушёваны временем до неузнаваемости. Но и для чёрного пессимизма всё–таки нет оснований. Если с традиционных позиций картина мира кажется запутанной безнадёжно, имеет смысл поменять позицию.

Сознание мыслителей, изучающих Солнечную систему, гипнотизировало согласованное движение небесных тел, гармония, царящая в системе.

Разумеется, движение в одной плоскости, совпадение собственного вращения планет и направления их движения вокруг Солнца с направлением вращения самого светила не могло быть случайным. Оно требовало объяснения в первую очередь и естественно наводило на мысль о совместном происхождении всего того, что составляет Солнечную систему. Отсюда единое облако, единый процесс.

Между тем вселенские события развивались, надо полагать, совсем по другому сценарию. Все крупные тела, входящие в Солнечную систему, планеты, кометы, астероиды, возникли в разное время независимо друг от друга и только позже, постепенно, по одному, индивидуально были захвачены Солнцем.

Идеи захвата, представления о формировании небесных систем в результате захвата возникали в истории астрономии неоднократно. Но в конце 19–го, начале 20–го веков астрономы пришли к заключению о невозможности захвата. Если они и допускали такую возможность, то лишь как маловероятную, при исключительных условиях взаимодействия с третьим телом. На идеи захвата было наложено жёсткое табу.

Думается, однако, что такое заключение было ошибочно. Захват возможен. Более того, он неизбежен. Вселенную надо понимать как пространство, более или менее равномерно заполненное хаотично перемещающимися телами различного объёма и массы. Разного рода ассоциации (планетные системы, звёздные скопления, галактики) – не более, чем островки в океане Вселенной. Вещество, приходящееся на скопления, составляет, вероятно, лишь доли процента от общей его массы. Решающая масса вещества Вселенной сосредоточена в свободных, не зарегулированных телах. Это строительный материал, который идёт на формирование небесных систем. Этого материала должно быть избыточно много, иначе Природе при её иррациональных, расточительных методах созидания, где всё решают Количество, Время и Случай, едва ли удалось бы создать что-либо достойное внимания. А между тем человеческому взору предстаёт удивительно стройная и сложная картина мира.

В движении свободных, не включённых в системы небесных объектов нет ни преимущественных скоростей, ни преимущественных направлений. Любые скорости, присущие материальным телам, любые плоскости и направления движений равновероятны и равновозможны. Эти одиночные объекты по ходу движения взаимодействуют друг с другом. По степени сложности возможны взаимодействия трёх порядков. Самая тривиальная форма, взаимодействие первого порядка – изменение направления движения объекта, отклонение от начального пути в результате притяжения другим объектом (рис. 1).

Взаимодействия первого порядка происходят постоянно. От скорости V движения тела m и минимального расстояния R min сближения с другим, более массивным телом M зависит угол изменения направления первого тела – угол поворота α. Он тем больше, чем меньше скорость тела V и расстояние до возмущающего объекта R min, и наоборот. При взаимодействиях первого порядка угол поворота α принимает значения от 0˚ до 90˚ исключительно –]0˚…90˚[.

Взаимодействия второго порядка – столкновения. Они происходят значительно реже. Тем не менее столкновение различных объектов – тоже рядовое, ординарное явление в небесной механике. Оно происходит в том случае, когда скорость приближающегося тела V и расстояние до возмущающего объекта R не достаточно велики и когда угол поворота первого тела α превышает 90˚ – α > 90°. (рис. 2).

Столкновения небесных объектов происходили всегда. Они продолжаются и ныне и происходят, что называется, на наших глазах. Солнечная система в Галактике не является изолированной зоной. Окрестности системы естественно, без каких бы то ни было границ, переходят в межзвёздное пространство. А это пространство не пустынно. Оно заполнено движущимися объектами. За время существования Солнца, а позднее и Солнечной системы, околосолнечное пространство множество раз во всех направлениях и с разными скоростями пересекалось телами различного объёма и массы. Абсолютное большинство этих тел покинуло пределы Солнечной системы, может быть, отклонившись от начального направления в результате взаимодействия с Солнцем или с крупными планетами (взаимодействие первого порядка). Значительная часть небесных тел, траектории движения которых пролегали в опасной близости от Солнца или других объектов, а скорости были недостаточно высоки, столкнулась с Солнцем или с какой–либо из планет, будучи притянута ими (взаимодействие второго порядка). И только очень малой доле посланцев космоса была уготована иная участь: они были захвачены Солнцем (планетами) и стали членами Солнечной системы (взаимодействие третьего порядка). На это указывает особая форма орбиты (либо её остаточные признаки) всех спутников Солнца, каковая может сложиться исключительно при захвате – эллипс с положением Солнца не в центре орбиты, а в области одного из его фокусов. Есть и другие наблюдательные признаки, есть и теоретические обоснования захвата, но они будут приведены позже.

Если учёные, исключающие возможность захвата, имеют в виду естественный выход спутника на орбиту, подобную планетной, то они несомненно правы. Захват такого рода действительно невозможен. Но в том-то и заключается великая тайна Природы, что первоначальная орбита свежезахваченного объекта совсем не похожа на классическую планетную орбиту. Знакомая нам планетная орбита, как и согласованное движение планет в системе – это результат эволюции продолжительностью в миллиарды лет.

Начальная орбита естественного спутника сильно вытянута и вообще подобна орбите долгопериодической кометы. Она не является правильным эллипсом и больше похожа на проекцию яйца с его тупым и острым концами, где разница в радиусах закруглений в начальный период очень существенна (рис. 3).

Солнце находится не в центре и не в фокусе "яйца". Оно смещено в область его тупого конца и помимо известного науке продольного имеет ещё и менее выраженное поперечное смещение относительно оси орбиты. Эти и другие особенности орбиты задаются способом её образования – захватом спутника.

Для того, чтобы небесное тело (система тел) смогло стать естественным спутником другого тела (системы тел), оно должно проходить на определённом расстоянии от объекта, осуществляющего захват (экспанта) со строго определённой скоростью. Это условие исчерпывающе описывается формулой захвата: Μ · γ = R · V².

Где М – масса экспанта (объекта, осуществляющего захват), кг;

γ – постоянная тяготения (γ = 6,67 · 10ˉ¹¹ м³/ кг. с²);

R – расстояние между взаимодействующими телами (среднее расстояние между спутником и экспантом на установившейся орбите), м;

V – средняя скорость движения спутника на орбите, м/с;

В формуле захвата γ и М – величины постоянные. Для любого экспанта

γ · Μ – константа захвата (γ · Μ = const). Для каждой отдельно взятой системы константа захвата имеет свою величину, которая определяется массой экспанта Μ. Значение массы спутника в захвате роли не играет. Не случайно в Солнечной системе в распределении планет по массе нет никакой последовательности. Из формулы захвата следует, что для захвата необходимо и достаточно выполнения одного условия: чтобы произведение среднего расстояния до экспанта на квадрат скорости спутника составляло вполне конкретную величину: R · V² = γ · Μ = const.

Условия захвата жёсткие. Но тем не менее захват возможен и он происходит. Как бы мала ни была вероятность определённого события, оно состоится, если возможно в принципе, и если хаотические события того же ряда в том же месте будут совершаться неопределённо долго.

Вероятно для захвата не требуется выполнения абсолютного равенства

R · V²= const. Абсолютное равенство недостижимо. Очевидно, существует определенное поле допуска, ширина которого пока неизвестна. Можно предположить,что захват возможен при условии равенства R ·V²= const ± 0,5 % ( от величины const). Наличие поля допуска заметно смягчает условия задачи.

Принято считать, что Солнечная система, Солнце, существует около 5 миллиардов лет. За это время Солнцем захвачено и сформировано 9 больших планет. Не так уж и много. Взаимодействие третьего порядка, захват, ординарным событием не назовёшь. Даже по астрономической шкале времени захваты происходят нечасто. И тем не менее спутники планет, спутники Солнца и звёзд, звёзды в скоплениях, звёзды в галактиках, галактики в скоплениях галактик, все естественные спутники других, более крупных объектов становятся таковыми только одним путём – в результате захвата. Других способов вывода спутника на орбиту Природа не знает.

Взаимодействие первого порядка, отклонение от начального пути, происходит при условии R · V² > const.

Взаимодействие второго порядка, столкновение, происходит при условии

R · V² < const.

Взаимодействие третьего порядка, захват, происходит при условии

R · V² = const.

Для Солнечной системы константа захвата Мc · γ составляет

13,21 · 10¹⁹ м³/с² при массе Солнца Мc = 1,98 · 10³⁰ кг.

В таблице № 1 приведены цифровые значения величин, которыми определяется динамическое равновесие в системе.

Таблица № 1

Система: Солнце – планеты

п/п	Планета	R ср. орбиты,м.	Скорость V, м/с	R·V², м³/с²
1.	Меркурий	5,7900·10¹⁰	4,7868·10⁴	13,27·10¹⁹
2.	Венера	1,0810·10¹¹	3,5011·10⁴	13,25·10¹⁹
3.	Земля	1,4950·10¹¹	2,9726·10⁴	13,21·10¹⁹
4.	Марс	2,2770·10¹¹	2,4086·10⁴	13,21·10¹⁹
5.	Юпитер	7,7760·10¹¹	1,3064·10⁴	13,27·10¹⁹
6.	Сатурн	1,4256·10¹²	9,6315·10³	13,22·10¹⁹
7.	Уран	2,8681·10¹²	6,7748·10³	13,16·10¹⁹
8.	Нептун	4,4941·10¹²	5,4303·10³	13,25·10¹⁹
9.	Плутон	5,8903·10¹²	4,7327·10³	13,19·10¹⁹

Произведение R · V² для всех планет очень близко к константе. Оно и понятно. При других условиях эти тела не могли бы стать спутниками Солнца. Некоторый разброс в итоговой графе находится, надо полагать, в пределах допуска. Абсолютное равенство R · V² = const наблюдается только у Земли и Марса.

Подобный расчёт проведён автором также и применительно к планетным спутниковым системам. Результат тот же. В каждой планетной системе для каждого экспанта и его спутников произведение R · V² с большой степенью точности (а для большинства спутников Сатурна и Юпитера – и с абсолютной точностью) приближается к константе захвата.

Средняя скорость спутника на орбите Vср. равняется исходной, собственной космической скорости в околосолнечном пространстве. Солнце, как и любой другой экспант, не повышает и не снижает скорости своих спутников. Оно только удерживает их на орбите. Энергия, за счёт которой спутник совершает вокруг Солнца свое бесконечное кружение, это собственная энергия тела, приобретённая им за пределами Солнечной системы.

a< 90° R · V² > const;

Рис 1. Взаимодействие первого порядка– отклонение.

α > 90º R · V² < const

Рис. 2. Взаимодействие второго порядка – столкновение.

R · V² = const Угол поворота α = 90˚ r1 >> r2 ; R1 > R2

Рис. 3. Взаимодействие третьего порядка – захват.

<<< на главную далее >>>